Algoritmos genéticos são uma família de modelos computacionais inspirados na evolução. Estes algoritmos modelam uma solução para um problema específico em uma estrutura de dados como a de um cromossomo e aplicam operadores que re-combinam estas estruturas preservando informações críticas.

Uma implementação do algoritmo genético começa com uma população (geralmente randômica) de cromossomos. Estas estruturas são então avaliadas para gerar oportunidades reprodutivas de forma que, cromossomos que representam uma solução "melhor" tenham maiores chances de se reproduzirem do que os que representam uma solução "pior". A definição de uma solução melhor ou pior é tipicamente relacionada à população atual.

Esta particular descrição to algoritmo genético é intencionalmente abstrata por que de certa forma, o termo algoritmo genético tem dois significados. Numa interpretação formal, o algoritmo genético refere-se ao modelo introduzido e estudado por John Holland (1975) e seus estudantes (e.g., DeJong, 1975). Ainda hoje a maior parte da teoria existente sobre algoritmos genéticos aplica-se totalmente ou primariamente ao modelo introduzido por Holland, assim como variações do que é referido em seu paper como algoritmo genético canônico. Avanços recentes na teoria da modelagem do algoritmo genético também aplicam-se primariamente ao algoritmo genético canônico (Vose, 1993).

Numa utilização mais abrangente do termo, um algoritmo genético é qualquer modelo baseado em população que utiliza operadores de seleção e re-combinação para gerar novos pontos amostrais em um espaço de busca. Muitos algoritmos genéticos foram introduzidos por pesquisadores de uma perspectiva experimental. A maior parte deles tem interesse no algoritmo genético como feramenta de otimização.

O objetivo deste tutorial é apresentar o algoritmo genético de forma que estudantes sem conhecimentos nesta área absorvam os conceitos basicos de algoritmos genéticos. O leitor mais sofisticado deveria conseguir absorver este material com relativa facilidade. O tutorial também trata de topicos como inversão, muitas vezes utilizados de forma errônea por pesquisadores novos neste ramo.

O tutorial inicia com uma discussão sobre otimização para introduzir as idéias da otimização e os conceitos básicos relativos ao algoritmo genético. Na seção 2 um algoritmo genético canônico é revisado. Na seção 3 o princípio de amostragem de hiperplanos é explorada e alguns operadores basicos de crossover são introduzidos. Na seção 4 varias versões do teorema do schema (schema-theorem) são discutidas. Na seção 5 alfabetos binarios e seus efeitos na amostragem de hiperplanos são considerados. Na seção 6 é considerado um breve criticismo ao teorema do schema e na seção 7 um modelo exato to algoritmo genético é desenvolvido. As últimas três seções tratam de formas alternativas de algoritmos genéticos e modelos computacionais evolucionários, incluindo implementações paralelas.

1.1 Codificações e problemas de otimização Índice

Geralmente existem dois componentes do algoritmo genético que são dependentes do problema: a codificação do problema e a função de avaliaço. Considere um problema de otimização de parâmetros em que devemos otimizar um conjunto de variáveis ou para maximizar um alvo (como lucro), ou para minimizar o custo ou uma medida de erro. Podemos considerar este problema como uma caixa preta com uma série de botões representando diferentes parâmetros; a única saída é o valor retornado por uma função de avaliação indicando quão bem uma combinação de parâmetros resolve o problema. O objetivo é setar os vários parâmetros para otimizar a saída. Em termos mais tradicionais, queremos maximizar (ou minimizar) uma função F(X1,X2, .. , Xm). Os algoritmos genéticos geralmetne tratam de problemas não lineares. Isto normalmente significa que não é possível tratar cada parâmetro como uma variável independente que pode ser resolvida isolada das outras variáveis. Existem interações que devem ser consideradas para maximizar ou minimizar a saída da caixa preta. Na comunidade do algoritmo genético, esta interação é geralemnte referida como epistase (epistasis). Geralmente a primeira coisa que assumimos é que as variáveis referentes aos paraâmetros podem ser representadas como sequências binárias (bit strings). Isto significa que as variáveis sao discretizadas em um intervalo correspondende a alguma potência de 2. Por exemplo, com 10 bits por parâmetro, podemos obter um intervalo com 1024 valores discretos. Se os parâmetros são realmente continuos esta discretização não é um problema. Isto assumindo que a discretização oferece resolução suficiente para possibilitar que a saída seja tão precisa quanto desejado. Também assume-se que esta discretização seja representativa da função subjacente. Se um parâmetro só pode assumir um conjunto finito de valores então esta codificação torna-se mais difícil. Suponha que, por exemplo, existão preicsamente 1200 valores discretos que podem ser atribuidos a uma variável Xi. Precisa-se então de pelo menos 11 bits para cobrir este intervalo e no entanto, isto codifica um total de 2048 valores. Os 818 padrões desnecessários podem resultar em uma não avaliação, uma avaliação padrão de pior caso, ou algumas possiblidades podem ser representadas duas vezes para que todas as sequências binárias resultem em um conjunto viável de valores. A solução deste tipo de problemas de codificação é geralmente considerada como parte do projeto da função de avaliaço. Além da questão da codificação, a função de avaliaço é geralmente considerada como parte da descrição do problema. Por outro lado, o desenvolvimento de um função de avaliaço pode muitas vezes envolver algum tipo de simulação. Em outros casos a avaliação pode se basear somente na performance representando somente uma avaliação parcial ou aproximada. Considere, por exemplo, uma aplicação de controle em que o sistema pode estar em um estado dentre um número exponencial de estados possíveis. Vamos assumir que um algoritmo genético é utilizado para otimizar algum tipo de estratégia de controle. Em casos como este, o espaço de estados deve ser modelado de maneira limitada, e a avaliação resultante da estratégia de controle é aproximada e barulhenta (c.f., Fitzpatrick and Grefenstette, 1988). A função de avaliaço deve também ser relativamente rapida. Isto é tipicamente verdade para um método de otimização, particularmente para algoritmos genéticos. Como um algoritmo genético trabalha com uma população de soluções potenciais, este incorre o custo de avaliar-se esta população. Além disto, a população é substituida (em parte ou totalmente) a cada geração. Os membros da população reproduzem e sua cria deve ser então avaliada. Se o algoritmo leva 1 hora para efetuar uma avaliação, ele levará mais de um ano para efetuar 10,000 avaliações. Isto seria aproximadamente 50 gerações para uma população de somente 200 sequências binárias

O primeiro passo na implementação do algoritmo genético é gerar a população inicial. No algoritmo genético canônico cada membro desta população é um string binário de comprimento L que corresponde à codificação do problema. Cada string destes é geralmente referenciado como genótipo ou cromossomo. Na maioria dos casos a população inicial é gerada randômicamente. Após ter sido criada a população inicial, cada membro é avaliado e recebe um valor de aptidão.

A função de avaliação e de aptidão deve ser bem distinguida. Neste tutorial a função de avaliação ou função objetivo provem uma medida de performance com respeito a um conjunto particular de parâmetros. E a função de aptidão transforma esta medida em alocação de oportunidades reprodutivas. A avaliação de um string representando um conjunto particular de parâmetros é independente da avaliação de qualquer outra string. Já a aptidão é sempre definida de acordo com outros membros da atual população

No algoritmo genético canônico, aptidão é definida como f_i/f onde f_i é a avaliação associada à i e f é a avaliação média de todas strings na população. A aptidão pode também ser associada à classificação de uma string na população ou outras medidas.

É útil olhar para a execução do algoritmo genético como um processo de duas fases. Inicia-se com a população atual, seleção é feita na população para criar uma população intermediaria. Então a população intermediaria sofre mutação e é recombinada para criar a próxima população. O processo de partir da população atual e chegar à próxima população constitui uma geração na execução do algoritmo genético.

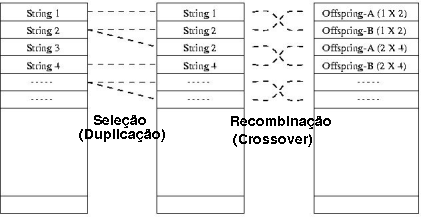
Uma geração é dividida em duas fases seleção e recombinação.

Vamos considerar primeiro a construção da população intermediária a partir da população atual. Após calcular f_i/f para todas as strings da população atual é feita a seleção. No algoritmo genético canônico a probabilidade que o cromossomo seja duplicado e posicionado na população intermediária é proporcional a aptidão. Existem diversas maneiras para efetuar o processo de seleção.

Após o término da construção da população intermediária a recombinação pode ocorrer. Isto pode ser visto como a criação da próxima população. É aplicado crossover à strings pareadas randomicamente com probabilidade denotada p_c (A população deveria estar devidamente embaralhada pelo processo randômico de seleção). Escolha um par de strings e, com probabilidade p_c recombine estas strings para formar duas novas que serão inseridas na próxima população.

Considere a seguinte sequência binária: 1101001100101101. A string representaria uma possível solução para algum problema de otimização de parâmetros. Novos pontos serão gerados recombinando duas strings. Considere a string 1101001100101101 e outra yxyyxyxxyyyxyxxy (x=0, y=1). Utilizando um único ponto de recombinação o 1-point crossover ocorre como segue:


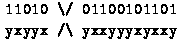
Trocando os fragmentos entre ambos produz a seguinte cria
11010yxxyyyxyxxy e yxyyx01100101101

Após a recombinação podemos aplicar um operador de mutação. Para cada bit na população mutamos com uma baixa probabilidade p_m. Tipicamente a probabilidade de mutação é aplicada com propbabilidade menor que 1%.

Após o processo de seleção, recombinação e mutação foram completos, a próxima população pode ser avaliada. O processo de seleção, recombinação e mutação formam uma geração na execução do algoritmo genético.